Authors: Bret R. Myers, Ph.D.1, Michael Burns2, Brian Q. Coughlin3, Edward Bolte4
1Department of Management and Operations, Villanova University, Villanova, PA, USA
2Villanova School of Business, Villanova University, Villanova, PA, USA
3Department of Athletics, Villanova University, Villanova PA, PA, USA
4Department of Athletics, Villanova University, Villanova PA, PA, USA
Corresponding Author:
Bret R. Myers, Ph.D.
800 E Lancaster Avenue
Villanova, PA 19085
bret.myers@villanova.edu
(804) 357-5876
Bret R. Myers, Ph.D. is a Professor of Practice in the Department of Management and Operations in the Villanova School of Business. His research interests focus on sports analytics, specifically, in the areas of team evaluation and managerial decision-making. He is also an Analytics Consultant for the Columbus Soccer Club of Major League Soccer
Michael Burns is an MBA Candidate and Graduate Research Fellow at Villanova School of Business. Michael is also the Director of Operations for the Men’s Soccer team at Villanova University.
Brian Q. Coughlin is the Director of Men’s Lacrosse Operations at Villanova and also has both a BBA and MBA from Villanova School of Business. Brian is also a Data Analyst at goPuff.
Edward Bolte is a student at Villanova University and student manager on the Lacrosse team. Edward is majoring in Civil Engineering
On the Development and Application of an Expected Goals Model for Lacrosse
ABSTRACT
The purpose of this study is to develop and apply an Expected Goals metric in lacrosse for team evaluation. Expected Goals is a metric that is used to represent the likelihood of a shot being a goal. The metric has gained traction in both soccer and hockey and has proven to add information and value in both team and player evaluations in both sports respectively. Like in soccer and hockey, the Expected Goals model for lacrosse in this paper is developed using logistic regression. Specifically, two metrics are created through this technique: 1) The standard Expected Goals model (xG) based on characteristics of the scoring opportunity before the shot is taken and 2) Post-shot Expected Goals (xGOT) which is updated to reflect whether or not the shot is on target.
Results: In terms of development, the logistic regression models used for the development of the xG and xGOT models both yield high levels of significance for fit (p < 0.001). The xG and xGOT metrics have higher correlations to team winning percentage (0.65 and 0.75) than their counterpart statistics of shots and shots on target. In terms of application, teams in the sample that had more xG than their opponents won 73% of the time as opposed to winning only 65% of the time when they outshoot their opponents. Similarly, teams in the sample that had more xGOT than their opponents won 71% of the time as opposed to only 62% of the time when they have more shots on target than their opponents. The evidence in this study suggests that using Expected Goals as a measure of attacking performance adds both value and information that can be useful for team evaluation.
Key Words: Sports Analytics, Team Evaluation, Sports Statistics
INTRODUCTION
With the growing sponsorship of technology and analytics in sports organizations, there is an opportunity to improve key performance indicators for team and player evaluation. The Expected Goals model (xG) is but one of many that has been implemented with great success thus far, though in many ways this modeling is still new and a work in progress. This type of model, most often implemented in the soccer and hockey realms, seeks to define shot quality and the probability that a certain type of shot could lead to a goal – either for or against the team in question (6). This probability can then be converted into a number that forecasts, given the array of shooting opportunities for a team in a game, the total number of goals that would have been expected to be scored. This is the essence of Expected Goals.
This paper applies the Expected Goals modeling framework in a unique way to lacrosse. After an extensive review of current xG literature, it appears our work is novel and can contribute to the sport. Consistent with many but not all models, our paper will employ logistic regression. The value of an xG model in lacrosse is in providing coaches with improved means of both team and player evaluation.
The Expected Goals metric is a relatively new statistic in the sports analytics world, but it has been implemented in many ways. First introduced by Macdonald at the MIT Sloan Sports Analytics Conference in 2012, this OLS regression model was created to better understand NHL player and team performance in a more isolated manner, meaning that the effect of other players on the ice was independent of a player’s individual rating. Macdonald felt this was a way to develop more appropriate and accurate metrics that address the scarcity of scoring goals without compromising the data. His work was well-received, and it has continued to be adjusted and modified to fit a varying level of statisticians’ needs including more predictor variables, applying a different type of regression, etc. (15). This was further developed using a ridge regression method and applied in a way that created an adjusted plus-minus statistic, as well as several other ratings, for hockey players (14).
It was not long after the introduction of this metric that xG modeling would be applied to football, or soccer as it is called in the US, in a very big way. Eggels was one of the first to pioneer the model for soccer in his thesis, where through logistic regression and a ranking system, he found that Expected Goals do accurately represent the probability of a scoring opportunity resulting in a goal and thus could be used to draw valuable insights into match results (9). Rathke continued to improve on the model by incorporating important qualities of shot opportunities like angle and distance from the goal (20). Fairchild et. al showed that a more in-depth model for Expected Goals and fractal dimensionality could be developed, using player-tracking data, to represent the probability of Expected Goals more precisely in soccer through a Poisson binomial distribution, ultimately enabling a more valuable interpretation of offensive and defensive efficiency (20). As Madrero, Brechot, and Flepp have most recently demonstrated, xG modeling is in a developmental phase and highly specialized models are still to be created, whether it be to revolutionize our understanding of Expected Goals alone or performance evaluation as a whole (5).
While the previous work noted was found in peer-reviewed journals, a large part of the xG literature is found in a less formal manner on many statisticians’ websites and blogs. A community of critique and mutual respect has developed between these different statisticians and their continually improving work contributes largely to the existing research on xG models. Altman, Bertin, and Caley are just a few of the key players in this field. Altman introduces a zoning system, that implements player tracking data and characterizes shots based on location, while also pitching a model that examines the pass leading up to the shot (2, 3). Though acknowledging that off-ball player location data could more fully develop his model, Caley showed that xG modeling “outperforms other shot-based systems in a variety of ways,” and he does this by creating a more in-depth zoning method than pitched by Altman (6). By running several varying regressions, Bertin was able to create an xG model, adjusted for more specific circumstances such as a game state variable (home team score – visiting team score) and header chances, that offered more significant results with a larger coefficient of determination (4). The continuous dialogue between these statisticians about their work serves as an extremely valuable building block for xG modeling moving forward. More on Expected Goals can be found at the American Soccer Analysis blog which validates their version of the xG model and details more ways in which such a model could be taken to the next level (7).
Since its introduction in 2012, expected goal metrics have been widely appreciated as revolutionizing the understanding of shooting opportunities, and performance in general, in sports with scoring scarcity. Our model is meant to build off previous work in the field and apply a similar methodology to the sport of lacrosse. With it, coaches can hopefully better understand and decompose team performance to optimize managerial decisions.
The participation rate in lacrosse, across all ages, has increased by 226% since 2001 (1). As a response to this growth – which has ultimately fueled a growth in the number of competitive lacrosse players seeking to play professionally today – brothers Paul and Mike Rabil founded the premier lacrosse league (PLL) in 2018. For the last two years, the PLL competed with the more established National Lacrosse League (NLL) and Major League Lacrosse (MLL) on signing athletes – NCAA division 1, 2, 3, and international talent. In December of 2020, the PLL and MLL announced a merger that effectively unified professional outdoor lacrosse. This has been but one of many ways to propel the sport forward in North America. Another method of doing that has been the implementation of a more integrative technological approach, including increased reliance on analytics and player performance data. In early 2019 for example, the MLL announced a partnership with Kinduct centered around improved analytics, player tracking tech, video tagging software, and more of the like (12). In late 2019, the NLL then announced its partnership with Sportlogiciq, a sports analytics leader that now collects, analyzes, and distributes live data as well as advanced statistics for the league (21).
Prior to these major partnerships and the acceptance of a need for data-driven decisions in professional lacrosse, there were minor surges in the level of interest in lacrosse analytics. Dating back as far as 2012, Coughlin introduced pace statistics as a means of calculating efficiency differences between teams that play at entirely different paces – measured by possessions per game (8). A few years later in 2016, McEwen demonstrated the stability of the shots per game metric year over year. He was able to prove that the number of shots, and/or shots on goal, are “more steady indicators of individual offensive success than goals scored” (17).
In order to appropriately develop a model for lacrosse, we had to ensure that some of the underlying sport-specific characteristics and metrics of previous models (primarily in hockey and soccer) would be comparable in lacrosse. For example, shot quality and the opportunity of chances had to be compared and was confirmed to be similar. Moreover, the quantity of shots per game (sample size) was a key statistic that we wanted to ensure lined up with or was greater than previous work. Because soccer and hockey are the two major sports where xG modeling has been applied, we compared their metrics to that of lacrosse. The former averages about 13-14 shots per team per game while the latter about 27-31 shots in the same interval(18, 19). Knowing that shot characterization from these sports to lacrosse is consistent, and that previous xG models were able to draw significant conclusions with their respective shot quantities, we determined that a model for lacrosse – averaging 43.8 shots per game – is appropriate.
Given the recent analytics developments in professional lacrosse and keeping in mind the approach to understanding the game demonstrated by Coughlin and McEwen, we saw this as the right time to promote that statistically based framework. We hope that the Expected Goals model can serve as the beginning of another, more sustainable implementation of statistics and analytics in the sport of lacrosse.
METHODS
Data Collection
The framework for this study begins with detailed data collection involving 4,497 lacrosse shots at the Division I college level across 28 different teams in the 2019 season. Collectively, 55 games are analyzed; however, 20 of the games involves the same team (given the affiliation of the data collectors). The following key variables are captured for every shot:
gameid (unique identifier for game), eventid (unique identifier for event within game), team (team name of shooting team), opponent (team name of defending team), Result (Goal, Off, Save), offPass (Y,N), Hand (L,R), X-Coordinate (horizontal dimension ranging from -25 to +25 left to right), Y-Coordinate (vertical dimension ranging from 0 to 83 with 0 being on the goal line).
Model Building
As mentioned earlier, the xG model for lacrosse is inspired by prior work done in soccer amd hockey. Accordingly, shot distance and shot angle are typical and predominant factors that are built into the model development. Shot distance is measured as the Euclidean distance between the shot location and the center of the goal mouth, while the shot angle is formed from location of shot to the two goal posts. Figure 1 below depicts how shot distance and angle are formed given the shot and goalmouth locations.
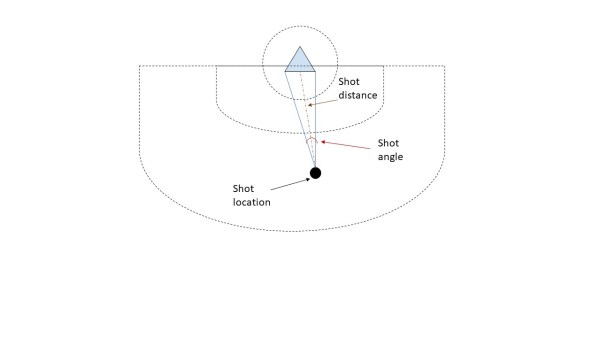
Figure 1
Note. The shot angle is formed from origin of shot to the two goal posts. The shot distance is the Euclidean distance from origin of shot to the center of the goal.
Empirical evidence suggests that goal conversion rates are significantly impacted by shot locations on the field. Figure 2 below is a heat map connecting shot location and goal conversion rates.
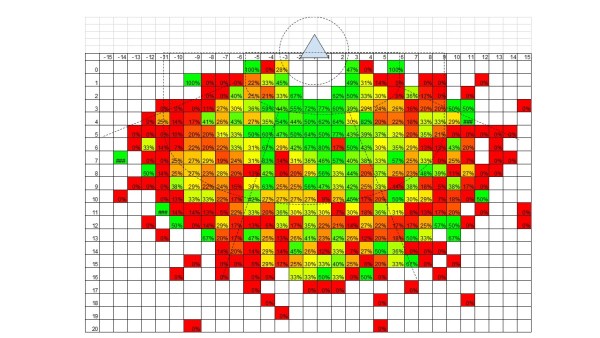
Figure 2
Note. This shot mapping depicts the goal conversion rates by location. Shots closer to the goals and tend to have a higher likelihood of scoring.
Model 1 – xG
The first of two models created is for the standard Expected Goals (xG). The binary target variable (Y) is whether or not a goal was scored on a shot (1 – goal, 0 – no goal). After examination of all key independent variables included, the final model is comprised of the following: X1 = Distance (yards), X2 = Angle (degrees), X3 = OffPass (Y – shot is off pass, N – shot is not off pass).
Using R, the following three predictor logistic model is carried out to determine significance.
The results from R are summarized in Table 1 below:
Table 1: Logistic regression coefficients for xG model
| Coefficents | Estimate |
| (Intercept) | -1.128*** |
| Distance | -0.051*** |
| Angle | 0.059*** |
| offPass | 0.342*** |
Overall, the model exhibits a high level of significance. As to the interpretation of the coefficients (given the null deviance of 5379.5 on 4363 df and residual deviance of 5094.0 on 4360 df) , the distance coefficient of -0.051 implies that for every additional meter away from the goal that the shot is, the odds of a goal decrease by about 5%. The shot angle coefficient of 0.059 implies that the odds of a goal increase about 6% for every additional degree in shot angle. The offPass coefficient of 0.35 implies that the odds of a goal increase about 42% when a shot occurs off the pass vs. not off the pass.
Model 2 – xGOT
The second of two models created involves the post-shot Expected Goals, otherwise known as Expected Goals on target (xGOT). With this model, off target shots automatically receive an xGOT value of 0. Again, the binary target variable (Y) is whether or not a goal was scored on a shot (1 – goal, 0 – no goal). The shots used for model fitting are conditioned for being on target. The same three predictor variables are included in the final model: X1 = Distance (meters), X2 = Angle (degrees), X3 = OffPass (Y – shot is off pass, N – shot is not off pass). Using R, the following three predictor logistic model is carried out to determine significance for the xGOT model:
The results from R are summarized in Table 2 below:
Table 2: Logistic regression coefficients for xGOT model
| Coefficents | Estimate |
| (Intercept) | -1.128 |
| Distance | -0.036** |
| Angle | 0.048*** |
| offPass | 0.340*** |
Like with xG, the xGOT model has a high level of significance. As to the interpretation of the coefficients (given null deviance of 3542.2 on 2558 df and residual deviance of 3409.5 on 2555 df , the distance coefficient of -0.04 implies that for every additional meter away from the goal that the shot is, the odds of a goal decrease by about 4%. The shot angle coefficient of 0.05 implies that the odds of a goal increase about 5% for every additional 1 degree in shot angle. The offPass coefficient of 0.34 implies that the odds of a goal increase about 40% when a shot occurs off the pass vs. not off the pass.
RESULTS
The model building process exhibits the significance of the logistic regression models in the development of the xG and XGOT metric. In application to the full data sets, both metrics perform well in measuring shot quality, as evidence by an increased association with success.
xG and xGOT average levels on goals vs. non-goals
One way to examine the significance of the xG and xGOT metrics is looking at average level splits in goal vs. non-goal occasions. Table 3 shows the xG and XGOT average levels for shots resulting in goals vs. shots resulting in non-goals:
Table 3: Average xG metric values on goals vs. non-goals (mean ± 95% C.I. margin of error).
| Shot Outcome | Average xG value | Average xGOT value |
| Goal | 0.35 ± 0.004 | 0.55 ± 0.018 |
| No Goal | 0.29 ± 0.008 | 0.20 ± 0.010 |
This summary indicates from the sample that shots that were goals had an average xG value of 0.35 vs. 0.29 for shots that were not goals. For xGOT, the split was even wider with goals having an xGOT value on average of 0.55 and non-goals have only 0.20 on average. Both of these splits are statistically significant (p-values virtually zero on 2 sample t-test) and are evidence to suggest that higher xG and xGOT valued-shots having higher associations with goal scoring outcomes.
xG and xGOT correlation to winning percentage
While the number of shots collected in the sample data set is large (n = 4,497), the number of teams involved is only 28, with only 14 having played at least 5 games. Based on the aggregated key statistics of the 14 teams in the sample, a correlation analysis is performed to examine the relationship between per game stats and winning percentage. Table 4 below summarizes the correlations of xG per game, xGOT per game, shots per game, and SOT per game to winning percentage:
Table 4: Correlation of xG statistics to winning vs. traditional metrics.
| Statistic | Correlation to Win Percentage |
| xGOT per game | 0.75 |
| xG per game | 0.65 |
| SOT per game | 0.44 |
| Shots per game | 0.13 |
The results reveal that xGOT per game and xG per game are more highly correlated with winning percentage than their counter parts (SOT per game and Shots). This shows the increased valued of using xGOT and xG as key performance indicators.
xG and xGOT game by game performance
Another way to look at the association between the xG and xGOT metrics and winning is through examination on a game-by-game level. Table 5 below provides a summary of game by game performance broken down by xG, xGOT, Shots, and SOT:
Table 5: Results of teams vs. their metric dominance over opponents
| Label | Wins | Losses | Win Percentage |
| Out xG opponent | 40 | 15 | 73% |
| Out xGOT opponent | 39 | 16 | 71% |
| Out Shot opponent | 36 | 19 | 65% |
| Out SOT opponent | 34 | 21 | 62% |
Again, xG and xGOT outperform their counterparts of Shots and SOT. Teams that had more xG than their opponent won 73% of the time vs. 65% when they solely outshot their opponent. Similarly, teams that had more xGOT than their opponent won 71% of the time vs. 62% for having more SOT than their opponent.
DISCUSSION
Overall, it is clear that xG and xGOT are meaningful metrics that can be used in lacrosse for the purpose of team evaluation. While the results indicate higher association to winning than traditional counterpart measures, they are not meant to replace them. Shots and Shots on Target are still valuable descriptive measures, and they differ from xG and xGOT in that they are tallies and more easily comprehended. The best application of xG and xGOT will be in combination with Shots and Shots on target. Accordingly, there is an opportunity to cross these metrics. For example, xG per shot can be used to describe the baseline threat level of the typical score chance for a team or player. In fact, teams that had a higher xG per shot than their opponent won 80% of the games in the sample. Another possibility that combines xG and xGOT is looking at the differential between the two (expressed as xGOT – xG). This would represent the increase in Expected Goals achieved by placing the shot on target. In fact, teams that have a higher differential on a game by game won 60% of the time and on the aggregate across games for each team, there is a 0.20 correlation with win percentage. While this is not as strong a key performance indicator as xG or xGOT alone, it could be meaningful as a way to measure how well teams executed their chances.
One limitation of this study is that the data sample only represents a subset of the larger NCAA Division I population. The sample predominantly consists of games played by a single program and those of regional opponents. Given the large number of shots and examination of 28 teams collectively, the information from this study is still useful and it is recommended for lacrosse teams to pursue xG and xGOT at any level of competition. In order to be positioned to calculate and apply the metric to shots, a team would need to chart the x,y coordinates (in yards) and also chart whether or not the shot came off a pass. It should be noted that law of cosines would need to be applied in order to find the shot angle detailed in this study.
CONCLUSIONS
The Expected Goals framework has its place in lacrosse as is exhibited by the development and application presented in this paper. It is important for clubs to capture and utilize the relevant data in order to emulate the proposed procedure. This can be done either with real-time logging of shot detail or retroactively through video. In sports like soccer and hockey that are more mature in the market for analytics and technology solutions, there are third party solutions that can provide the detail necessary for an xG model, and even go as far to provide the metric and other relevant derivatives through developed platforms and reports. What is unique about this study is that the data was collected first hand by the staff of a Division I college program, which required a significant investment in time given the manual processing. However, this demonstrates that both college and professional programs could employ a low-cost solution to track the metric for their own team performances. The results of this paper show the value-added in additional information gain and an improved set of key performance indicators that can be used to evaluate team performance
APPLICATIONS IN SPORT
The findings in the paper demonstrate the versality of the Expected Goals model to be applicable to the sport of Lacrosse. Given the appropriate data collection. Coaches and other key management personnel can use xG for better team evaluation and understanding of performance. While the focus of the sample is representative of a limited set of Division I college games, the methodology can easily be applied to other data sets across various levels of competition.
REFERENCES
- 2017 Participation Survey (p. 8). (2017). [Annual Report]. US Lacrosse.
- Altman, D. (2014, December 24). Expected Goals from situations [Blog]. North Yard Analytics. http://www.northyardanalytics.com/blog/2014/12/24/expected-goals-from-situations/
- Altman, D. (2015). Beyond shots: A new approach to quantifying scoring opportunities. Opta Pro Forum. https://northyardanalytics.com/Dan-Altman-NYA-OptaPro-Forum-2015.pdf
- Bertin, M. (2015, August). The Third-to-Last Thing I’ll Ever Write About Expected Goals [Blog]. Numbers and Stuff. http://michaelbertin.com/2015/08/28/the-third-to-last-thing-ill-ever-write-about-expected-goals/
- Brechot, M., & Flepp, R. (2020). Dealing With Randomness in Match Outcomes: How to Rethink Performance Evaluation in European Club Football Using Expected Goals. Journal of Sports Economics, 21(4), 335–362. https://doi.org/10.1177/1527002519897962
- Caley, M. (2015, April 10). Let’s talk about Expected Goals. SB Nation | Cartilage Free Captain. https://cartilagefreecaptain.sbnation.com/2015/4/10/8381071/football-statistics-expected-goals-michael-caley-deadspin
- Cheuk, H. H., McKinley, E., & Moore, J. (2018, August 29). The Next Level of xG: Expected Possession Goals. American Soccer Analysis. https://www.americansocceranalysis.com/home/2018/8/28/expected-possession-goals-part-1
- Coughlin, B. (n.d.). Introduction to Pace Statistics: The Most Efficient Offenses in the Nation [Forum]. Inside Lacrosse. Retrieved April 28, 2021, from https://www.insidelacrosse.com/article/introduction-to-pace-statistics-the-most-efficient-offenses-in-the-nation/12790
- Eggels, H. (2016). Expected Goals in soccer: Explaining match results using predictive analytics. Eindhoven University of Technology.
- Fairchild, A., Pelechrinis, K., & Kokkodis, M. (2018). Spatial analysis of shots in MLS: A model for Expected Goals and fractal dimensionality. Journal of Sports Analytics, 4(3), 165–174. https://doi.org/10.3233/JSA-170207
- Keegan, J. (2021, February 25). 10 Man Ride: Expected Goals (xG) Model. Premier Lacrosse League. https://premierlacrosseleague.com/articles/10-man-ride-expected-goals-xg-model
- Kinduct Signs As The Official Health And Performance Software Platform Of MLL. (n.d.). Major League Lacrosse. Retrieved October 12, 2020, from https://majorleaguelacrosse.com/news/2019/3/3/kinduct-signs-as-the-official-health-and-performance-software-platform-of-mll.aspx?path=mlax
- Kullowatz, M. (2017, March 8). Validating the ASA xGoals Model [Blog]. American Soccer Analysis. https://www.americansocceranalysis.com/home/2017/3/6/validating-the-asa-xgoals-model
- Macdonald, B. (2012a). Adjusted Plus-Minus for NHL Players using Ridge Regression with Goals, Shots, Fenwick, and Corsi. Journal of Quantitative Analysis in Sports, 8(3). https://doi.org/10.1515/1559-0410.1447
- Macdonald, B. (2012b). An Expected Goals Model for Evaluating NHL Teams and Players. 8.
- Madrero, P. (2020). Creating a Model for Expected Goals in Football using Qualitative Player Information. Universitat Politecnica de Cataluyna.
- McEwen, P. (2016, November 29). Analyzing NLL Shooting Numbers. Medium. https://medium.com/@pmcewen/analyzing-nll-shooting-numbers-2c17a9204dd3
- NHL League Averages. (2021). Hockey Reference. https://www.hockey-reference.com/leagues/stats.html
- Pugsley, D., & Knutson, T. (2013, January 17). A Deeper Look At Shots on Target. SB Nation | Bitter & Blue. https://bitterandblue.sbnation.com/2013/1/17/3880454/a-look-at-shots-on-target-epl
- Rathke, A. (2017). An examination of Expected Goals and shot efficiency in soccer. Journal of Human Sport and Exercise, 12(Proc2), 16. https://doi.org/10.14198/jhse.2017.12.Proc2.05
- Sportlogiq Becomes the Official Statistics Partner of the National Lacrosse League. (2019, November 6). NLL. https://www.nll.com/news/sportlogiq_partner/
.

